近年來,深度學習技術在多個領域實現了突破性進展,從語言處理到影像識別,無不體現了其強大的學習能力。而在這一進步的核心,多層感知器(MLP)一直扮演著基石的角色。MLP,也被稱為全連接前饋神經網絡,是深度學習模型的基礎構建塊,用於逼近非線性函數。其重要性不言而喻,因為它們是機器學習中用於逼近非線性函數的默認方法。然而,儘管MLP在各個方面都顯示出了其不可替代的價值,但在解釋性和參數效率方面,它面臨著一定的挑戰。尤其是在與當今流行的模型如Transformers結合時,MLP在沒有後處理分析工具的情況下,相對於注意力層,其可解釋性較差。
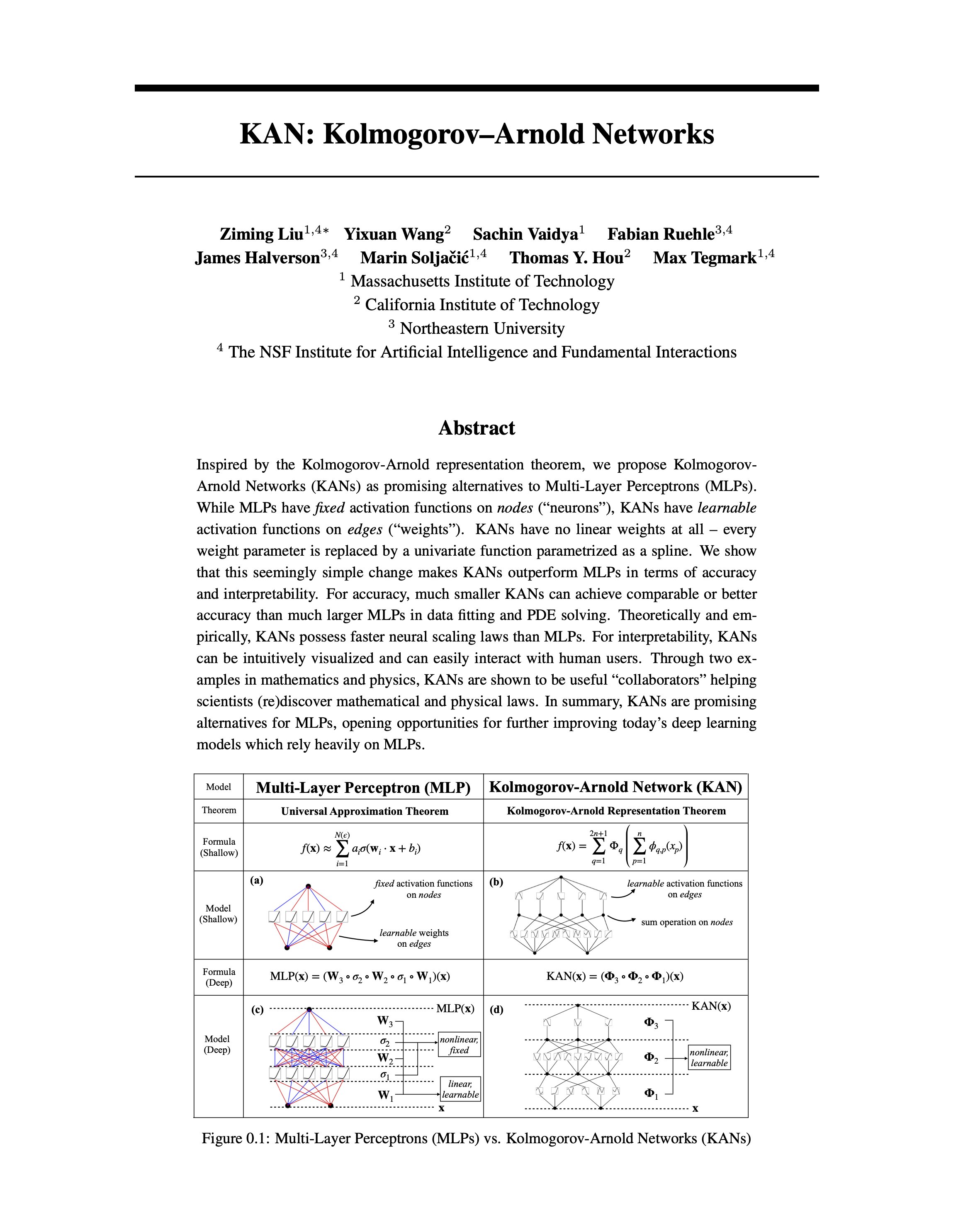
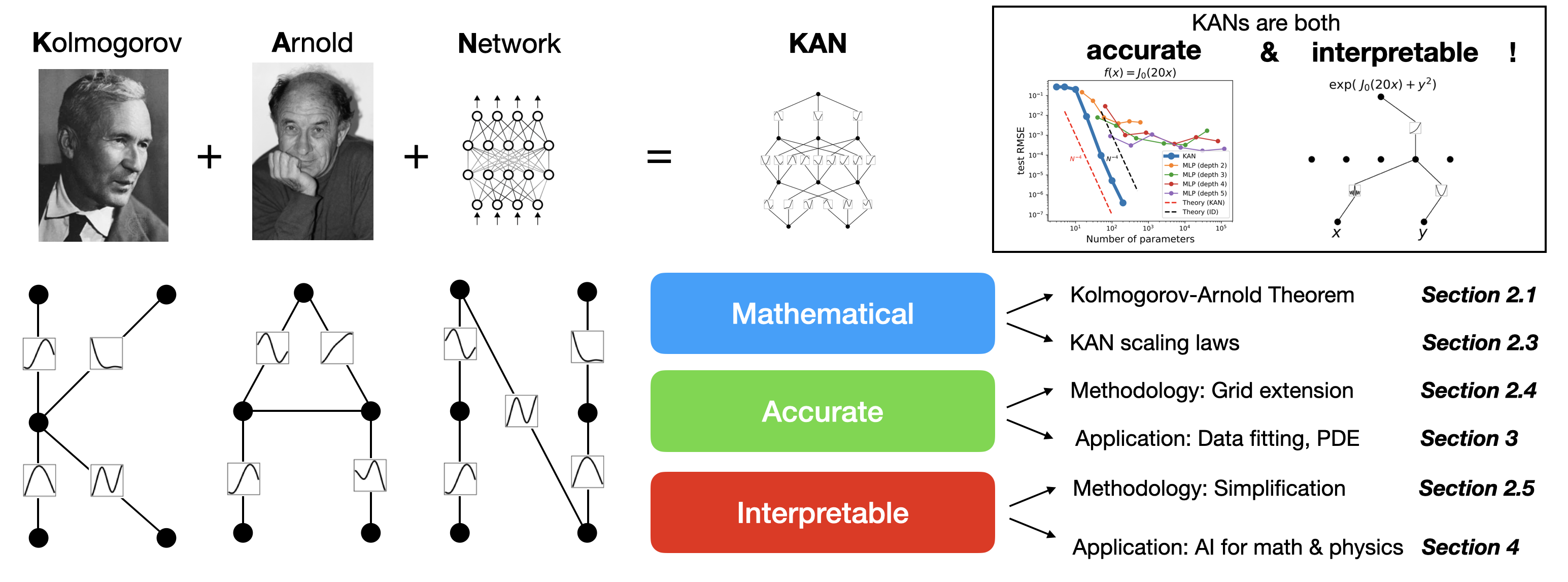
面對這些挑戰,Kolmogorov-Arnold Networks(KAN)的概念應運而生。KAN靈感來源於Kolmogorov-Arnold表示定理,提出了一種全新的思路來構建深度學習模型。與傳統MLP不同,KAN在邊(權重)上放置可學習的激活函數,完全沒有線性權重矩陣:每個權重參數都被替換為一個可學習的一維函數,參數化為樣條(spline)。這一設計不僅呈現出了KAN與MLP之間的根本區別,而且展示了在參數效率和模型精度方面KAN潛在的巨大優勢。

KAN的提出,不僅挑戰了傳統MLP模型,也為未來的模型創新提供了新的方向。將KAN與當前流行的模型,如Transformers結合,創造出「Kansformers」,可能會進一步推動深度學習的發展。此外,KAN在計算成本上雖然可能高於傳統MLP,但其在模型精度和參數效率方面的表現,展示了KAN潛在的巨大優勢。特別是在一些特定的學習任務上,如偏微分方程求解和連續學習中,KAN顯示出比MLP更優的性能。
這一切都表明,深度學習領域正處於一個新的轉折點。KAN的出現,開啟了深度學習未來發展的新思考,其獨特的設計思路引發了學術界和工業界的廣泛討論。從MLP到KAN,這不僅僅是模型架構的革命,更是對深度學習模型設計思維的一次重大轉變。隨著深度學習技術的不斷進步,對模型的要求也在不斷提高,KAN的提出為未來的模型創新提供了新的方向,展示了深度學習技術面向未來的無限可能。
在探索深度學習的進化過程中,我們見證了從多層感知器(MLP)到 Kolmogorov-Arnold Networks(KAN)的重大轉變。這一轉變不僅是技術上的創新,更是對深度學習模型設計思維的根本變革。本節將深入探討 MLP 和 KAN 的基本原理以及它們之間的關鍵差異,揭示這場革命序幕背後的科學意義。
本文大綱
MLP 的局限性與挑戰
多層感知器(MLP)是現代深度學習模型的重要基石,它通過全連接的前饋神經網絡逼近非線性函數,對於各類學習任務都有著不可替代的價值。然而,MLP 在處理複雜數據結構時顯示出其局限性,尤其是在模型可解釋性和參數效率方面。傳統的 MLP 模型依賴於線性權重矩陣和固定激活函數,這限制了模型在某些特定學習任務上的性能表現。
可解釋性的挑戰
在與當前流行的模型如 Transformers 結合時,MLP 由於缺乏直接的後處理分析工具,與注意力層相比,其可解釋性較差。這一局限性在複雜的數據分析和決策過程中,尤其成為研究和應用的瓶頸。
參數效率的考量
儘管 MLP 在逼近非線性函數方面極具價值,但其結構設計在參數效率方面存在明顯的劣勢。大量的線性權重參數和全連接層的使用在一定程度上增加了模型的複雜度,而沒有帶來相應的性能提升。
KAN 的創新與優勢
Kolmogorov-Arnold Networks(KAN)的提出,標誌著深度學習模型設計的一次革命。KAN 的設計思路源於 Kolmogorov-Arnold 表示定理,其將傳統的線性權重參數轉化為可學習的一維函數,徹底改變了模型的結構設計。
突破參數效率的限制
KAN 的突出特點是在邊(權重)上放置可學習的激活函數,完全沒有線性權重矩陣。這種設計大幅提高了模型的參數效率,每個權重參數都被一個可學習的一維函數所替代,使得模型對於給定的學習任務能夠以更少的參數實現更高的精度。
強化模型的可解釋性
相較於 MLP,KAN 由於其獨特的結構設計,在提升模型性能的同時,也大幅增強了模型的可解釋性。KAN 通過將每個傳統的線性權重參數轉化為可學習的一維函數,為模型提供了一種新的視角來理解數據之間的關係。
應用領域的擴展
KAN 的提出不僅挑戰了傳統 MLP 模型,也為深度學習模型的應用提供了新的方向。在特定的學習任務如偏微分方程求解和連續學習中,KAN 顯示出比 MLP 更優的性能,開啟了深度學習技術應用的新篇章。

總結來說,從 MLP 到 KAN 的轉變不僅是模型架構的革命,更是對深度學習模型設計思維的一次重大轉變。KAN 的提出為深度學習技術的未來發展提供了新的方向,展示了構建高效、可解釋性強的深度學習模型的無限可能。
在探索深度學習的新篇章中,Kolmogorov-Arnold Networks(KAN)的出現標誌著一次顯著的技術突破。本章節將深入探討 KAN 在各領域應用的突破和可能性,從而揭示其對於未來深度學習技術發展的影響。
KAN 的技術突破
KAN 的設計靈感來自於 Kolmogorov-Arnold 表示定理,這一理論基礎使其在多個層面上遠超傳統多層感知器(MLP)。首先,KAN 的結構創新在於將傳統的線性權重參數轉化為可學習的一維函數,這一變革提升了模型在參數效率和精確度上的表現。其次,這種結構設計還增強了模型的可解釋性,使得 KAN 在數據分析和決策過程中成為一個更加強大的工具。
KAN 與 MLP 的比較
在參數效率方面,KAN 通過其創新的結構設計實現了對參數的高效利用,與傳統 MLP 模型相比,KAN 能夠在更少的參數下達到更高的學習精度。此外,KAN 的可解釋性在某些應用場景中是一項關鍵優勢,特別是在需要洞察數據背後深層次關聯的場合。
| 特性 | MLP | KAN |
|---|---|---|
| 結構 | 全連接前饋 | 基於函數的權重 |
| 可解釋性 | 相對較差 | 強 |
| 參數效率 | 一般 | 高 |
| 應用領域 | 廣泛 | 特定領域能力突出 |
| 設計思路 | 傳統 | 創新 |

KAN 在特定領域的應用潛力
KAN 在特定學習任務上的表現尤為優異,例如在偏微分方程求解和連續學習中,其展現出的性能超越了傳統 MLP。這一點對於需要高度精度和效率的科學計算和工程應用尤為重要。
案例分析:偏微分方程求解
在偏微分方程求解的應用中,KAN 的獨特結構設計使其能夠更有效地處理複雜的數學模型,從而提供更精確的解。這種能力為工程和自然科學研究提供了新的工具,尤其是在需要高度數學模擬和預測的領域。
連續學習的應用
在連續學習的領域,KAN 展現出了對於學習任務的持續適應能力,這對於機器學習模型來說是一個重要的進步。通過有效地利用以往學習的知識,KAN 能夠在新的學習任務上快速適應,顯示出比傳統 MLP 更好的學習效率。
KAN 的這些技術突破和應用潛力,展示了其在推動深度學習技術發展方面的重要價值。從 MLP 到 KAN 的轉變,不僅是模型架構的一次重大變革,更是對深度學習模型設計思維的根本革新。隨著深度學習技術的不斷進步,KAN 的提出為未來模型創新提供了新的方向,為深度學習技術的未來發展開啟了新的可能性。
隨著深度學習技術的不斷進步,對模型的要求也在不斷提高。在這個過程中,傳統的多層感知器(MLP)模型在處理複雜的數據結構和提升解釋性方面顯示出了其局限性。因此,深度學習領域迫切需要新的創新思路和模型架構來應對這些挑戰。近年來,Kolmogorov-Arnold Networks(KAN)的提出,不僅展示了一種全新的模型架構,同時也為未來的模型創新提供了新的方向。將 KAN 與當下流行的模型,如 Transformers 結合,創造出的「Kansformers」,無疑將會進一步推動深度學習技術的發展。
從 MLP 到 KAN:顛覆傳統思維
在深度學習的歷史中,MLP 一直是基礎且重要的模型架構,在許多領域都有著廣泛的應用。然而,當涉及到解釋性和參數效率問題時,MLP 的局限性就凸顯出來。相對於 MLP,KAN 通過在權重上放置可學習的激活函數,完全沒有線性權重矩陣,這一創新設計不僅提高了模型的參數效率,還增強了模型的可解釋性。這種從根本上改變模型架構的思維,為深度學習技術的未來發展提供了新的可能性。
在未來,我們可以預見到 KAN 和 Kansformers 在深度學習領域將扮演越來越重要的角色。不僅僅是在模型架構的創新上,更在於它們如何推動深度學習技術在更廣泛的應用領域中的發展。隨著對這些新型模型的深入研究和應用探索,深度學習技術的未來將變得更加精彩。
在對深度學習技術的未來探索中,Kolmogorov-Arnold Networks(KAN)的出現,無疑是一次重大的突破。它不僅挑戰了傳統 MLP(多層感知器)的架構,也為深度學習模型的進一步發展提供了新的方向。隨著時間進入到 2024 年及以後,深度學習領域持續迎來新的技術革新,其中,將 KAN 與當前流行的模型如 Transformers 結合,創造出的「Kansformers」,預示著深度學習技術的新浪潮。
KAN 的技術創新與挑戰
KAN 的提出,基於 Kolmogorov-Arnold 表示定理,通過將每個傳統的線性權重參數轉化為可學習的一維函數,從而提高了模型的參數效率和精確度。這一創新不僅解決了傳統 MLP 在解釋性和參數效率方面的限制,而且在處理特定學習任務,如偏微分方程求解和連續學習中展示出更優異的性能。
然而,KAN 在計算成本上可能會高於傳統 MLP,這對於需要大規模應用和快速迭代的場景可能會是一個挑戰。對於這一挑戰,學術界和工業界需要共同探索,通過技術創新和算法優化來克服。

未來展望:從 KAN 到 Kansformers
KAN 的提出不僅是對傳統 MLP 模型的挑戰,也為未來模型創新提供了新的方向。特別是將 KAN 與目前流行的 Transformers 模型結合,創造出的「Kansformers」,有望成為推動深度學習技術發展的重要力量。這種結合不僅在模型精度和參數效率上有所改進,更重要的是,它開啟了深度學習模型設計的新思維,為探索更高效、可解釋的深度學習模型提供了無限的可能性。
呼籲與期待
面對深度學習技術的這次重大革新,學術界和工業界的研究人員應共同探索 KAN 的潛力,推動深度學習技術的進一步發展。這不僅僅是模型架構的一次創新,更是對深度學習模型設計思維的一次重大轉變。我們期待 KAN 和 Kansformers 在未來在深度學習領域扮演更重要的角色,不僅在模型架構的創新上,更在於它們如何推動深度學習技術在更廣泛的應用領域中的發展。
隨著對這些新型模型的深入研究和應用探索,深度學習技術的未來將變得更加精彩。面對技術革新,我們不僅需要積極應對挑戰,更應擁抱變化,共同探索深度學習技術面向未來的無限可能。